Conservative and non-conservative forces

LEARNING OBJECTIVE 3.4.C - Describe how the selection of a system determines whether the energy of that system changes.
AP MECHANICS -C LEARNING OBJECTIVE CON 1.A -Compare conservative and dissipative forces.
Describe the role of a conservative force or a dissipative force in a dynamic system.

In the last section, we looked at the case of motion of a ball in the gravitational field and concluded that the total ME of the ball remains conserved during its motion.

Now extending our argument along the lines of the law of conservation of mechanical energy, we can say that gravitational potential energy works well within the limitations of the law of conservation of mechanical energy. To say:

Gravitational force is a conservative force.

Conservative force

Why, because during the motion of the ball in the gravitational field, the direction of the velocity has been reversed at the same value of x, but there has been no loss or gain of kinetic energy for each and every point during its motion. In such a case the force is said to be Conservative forces.

The forces or potential energy functions U(x) which satisfy this requirement can be said to fall within the limit of the law of conservation of mechanical energy. All other forces are called Non-conservative forces.

Conditions for a conservative property of forces

Under what conditions does the force have this conservative property?

Will the force F(x) which depends on the direction of motion of the object to which it is applied, be conservative or non-conservative? One such example of force we all are familiar with is friction or in general resistive forces. Resistive forces emerge to oppose the relative motion. Hence, they always act in the opposite direction of relative motion. This means they always do negative work on the object they act on.

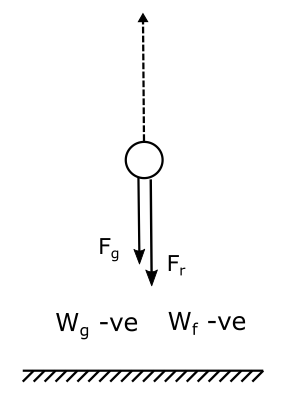
Let’s consider our last case of the ball thrown in the air. If there was an air resistance (a resistive force) during the motion. We can say while the ball was in the:

Upward journey: Resistive force will do negative work as it acts downward, opposite to the displacement of the ball. Similarly, gravity is also doing negative work.

Downward journey: Resistive force will again do negative work as it acts upwards this time, again opposite to the displacement of the ball. Gravity though will do positive work this time as the direction of force and displacement are the same.

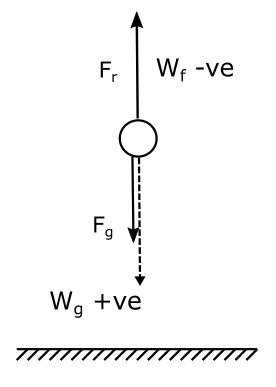
The negative and positive work done by gravity eventually sum to zero for the whole journey. But the work done by the resistive force will be net negative. Hence the kinetic energy of the ball has to be reduced to compensate for this negative work and the total ME will decrease.

Hence, Resistive forces such as friction, air resistance, and viscous forces are non-conservative forces. We cannot use the law of conservation of mechanical energy if these forces are present.

Non-conservative forces

So, what determines if the force is a conservative or non-conservative? The crucial feature is, indeed, that the net work done by F(x) should be zero over any journey beginning and ending at any given value of x.

Gravitational force satisfies this requirement, while the resistive force doesn’t. Only if this condition is satisfied can one define a potential energy function.

A potential energy function U(x) can only be defined for conservative forces. The condition of zero net work over any closed path defines a conservative force in all circumstances and should be remembered as a basic definition.

The fundamentally valid definition of the conservative forces or associated potential energy function U(x) is that net work done by these forces must be equal to zero in on a closed path. What this means is that if there is a body moving under the conservative forces only, and it returns to the point of start the net work done by the force must be zero. In Figure 5, a body at position A is moved around several positions and brought back to point A, net work done = zero.