AP MECHANICS -C LEARNING OBJECTIVE CON 1.A -. Describe the role of a conservative force or a dissipative force in a dynamic system.
Does the work done by a conservative force depend upon the trajectory or path? Suppose a conservative force of constant magnitude F acts downwards. Under the influence of this force, an object moves along a curved path from point A to point B. How much work is done?
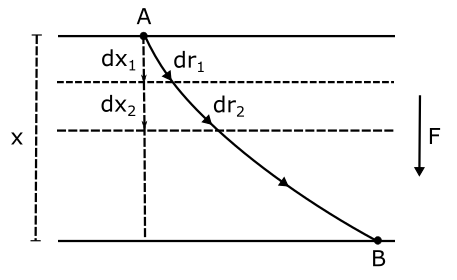
Clearly, the force is always acting vertically downwards at all points during the motion of the body. In order to compute the work done we will need to find the product of force and displacement along the line of the force. Let’s break down the displacement into n small segments $dr_1$, $dr_2$ and so on to $dr_n$. The projection of these displacements along the line of force that is the vertical distance will be then $dx_1$, $dx_2$ and so on to $dx_n$. The net work done will be then equal to the sum product:
$W = F( dx_1 ) + F( dx_2 ) + … + F( dx_n ) = F ( dx_1+dx_2+…+ dx_n )$
The second term is nothing but the total vertical distance x. What it means is that you can choose to move the body through any path between the two points A and B lying on different heights, the net work done will be the same for all the paths or trajectories. The path you choose doesn’t matter, all that matters is the vertical separation of the points.
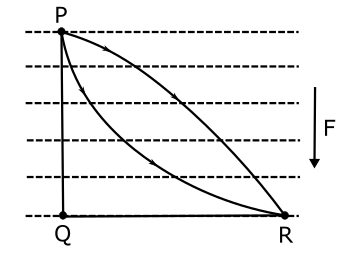
Let me illustrate this important concept through an example. Suppose an object moves from point P to R through three different paths two curved and one combination of straight lines ( PQR via Q), What will be the work done through different paths? We have just proved that all that matters is the vertical separation of P and Q as the force acting on the body is in the vertical direction. The work done by the force F will be exactly the same. Even if we choose to take the particle through back-and-forth paths or any complicated path. The work done will be the same for all of them. Ref to Figure 8, work done by force F in motion from P to Q through paths P1 and P2 will be the same.
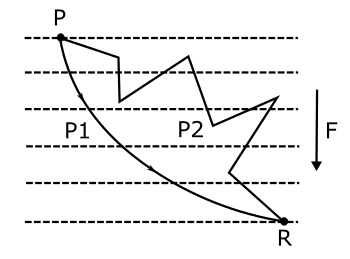
Work done during the motion of a particle from point 1 to point 2 is independent of the path through which it travels, given the force doing work is conservative.
Independence of work done on path in case of conservative force