When can we use conservation of mechanical energy?

LEARNING OBJECTIVE 3.4.B - Describe the behavior of a system using conservation of mechanical energy principles.
AP MECHANICS -C LEARNING OBJECTIVE CON 1.A -Compare conservative and dissipative forces.
Describe the role of a conservative force or a dissipative force in a dynamic system.

In last section, we looked at the law of conservation of mechanical energy. Then we quickly dismissed it in favor of most border law: the law of conservation of energy.

Let’s now take a step back and consider the law of conservation of mechanical energy once again, because in Physics many of the systems we consider for analysis are free from imperfections such as friction and resistive forces, or we simply ignore them in the idealized world. In such cases, we can still use the law of conservation of mechanical energy to solve mechanics problems without worrying about calculating forces or accelerations. In such a situation, this law could be a very powerful and efficient tool.

law of conservation of mechanical energy states that if there are no external forces acting on the system and in the absence of friction and resistive forces the total mechanical energy of the system remains constant or conserved.

$ ME = KE + U = \mbox{Constant}$

Mechanical Energy of a closed system = Kinetic Energy + Potential Energy = Constant or Conserved

When can we use the law of conservation of mechanical energy ?

In order to understand when we can use the law of conservation of mechanical energy, let’s resort to some mathematics.

Mathematically, we can express this law as:

$\frac{mv^2}{2} + U (x) = ME $

In the above expression, we have used $mv^2/2$ for KE and U(x) to represent potential energy. By definition, potential energy depends upon the position or simply distance from the origin, hence it will be a function of position x, hence U(x). Now, let’s rearrange this equation to find the value of v.

$v^2 = {\frac{2 [ME – U (x)] }{m}}$

This is a quadratic equation that has two equal and opposite roots. One positive and one negative.

$v = +- \sqrt{\frac{2 [ME – U (x)] }{m}}$

What it means is that if the ME is a constant, that is to say, the law of conservation of mechanical energy holds, the potential energy U(x) is restricted to have a function which gives a unique value for every value of x, so that the value of v finally should have two equal and opposite values. Let me explain this with an example.

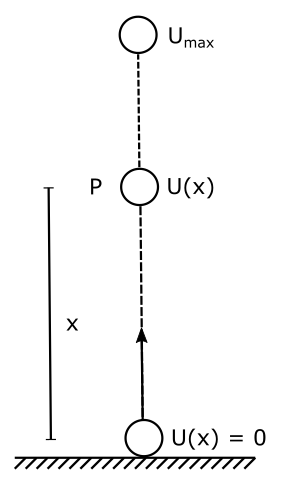
When we throw a ball vertically up, the value of potential energy changes at each and every point on the trajectory of the ball, refer to Figure. The potential energy has a zero value initially and it increases linearly as the ball progresses along its trajectory upward. At the top of its trajectory, potential energy has a maximum value. This means potential energy varies from point to point as a function of distance, if we say put the x coordinate along the path, this potential energy can be represented as a function of x as U(x).

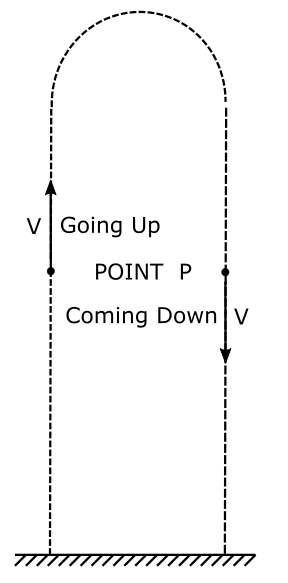
Let’s consider an arbitrary point P on the trajectory of the ball and observe how the velocity of the ball changes at this point. While the ball travels up, and passes point P, it had a velocity v directed upwards. When the ball travels down it ball has a velocity v ( same magnitude) directed downwards. Two equal and opposite values. Hence, the requirements of ME conservation are met in this case and we can conclude:

The gravitational potential energy U(x), works well within the limitations of the law of conservation of mechanical energy.

Gravitational potential energy

Surely, the energy which gets stored as potential energy can also be described through the force. The work which we do to impart kinetic energy to the ball eventually gets stored as gravitational potential energy. This stored energy is then released back in the form of kinetic energy when the ball starts to descend, allowing the ball to return back with the exact same kinetic energy as before. Indeed at all the points during its trajectory, it posed the exactly same amount of kinetic energy whether it was going up or down.

In the next section, we will extend this idea from potential energy to forces. This will allow us to define two kinds of force conservative and non-conservative forces.