LEARNING OBJECTIVE : 7.1 Describe Simple harmonic motion 7.2 Describe the frequency and period of an object exhibiting SHM.
Consider the following motions:
An object pushed on a frictionless surface: The object will start moving as the work done by the person pushing it converts into the kinetic energy of the object. The object will continue to move in one direction continuously unless disturbed.
An object tied to a string and free to rotate around a pivot point: If someone imparts sufficient velocity to this object, the object will start to rotate in a circular motion and will continue to do so forever, unless disturbed.
The first example is of translational motion and the second is that of rotational motion, they will progress in one direction continuously unless disturbed. It is, however, also possible for a motion to progress first in one direction and then opposite. The change in direction may happen after a long interval and sometimes at short intervals or even at very short intervals.
Such an alternate movement in opposite directions is called vibration (from Latin word meaning shake).
What is vibrartion?
This type of motion is very common in nature and here are few examples, you may be aware of already:
- Swaying or trembling of branches and leaves in the wind
- The swinging of a pendulum.
- The movement of a swing.
- The motion of sound waves.
- The movement of a guitar string while playing it.
- The movement of our vocal cords.
- A body attached to a spring
The form of vibration that was first studied by scientists was that of a taut string when plucked. Such strings were used in musical instruments known even to the ancients. The plucked strings give rise to musical sounds for reasons involving the vibratory motions lent by the vibrating strings to the air itself. The ancient Greek mathematician and philosopher Pythagoras was the first to study such vibrations. His interest lay entirely in the relationship of these vibrations to music, and as a result:
Vibratory motion is frequently called harmonic motion.
SHM
Most vibratory motion is of a complicated nature and does not readily lend itself to easy mathematical analysis. A particular type of vibratory motion can be analyzed using elementary mathematics. Some of examples of these motions are a taut vibrating string, a body attached to an elastic spring etc. These kinds of motion are therefore called “simple harmonic motion (SHM).
Consider for example, motion of a block attached to an elastic spring and which for simplicity rests on a frictionless floor.
If we move the block towards right and then release, then we will find that block starts to move towards left due to action of elastic forces of the spring and when it reaches a point where spring is not stretched this force vanishes (as spring is no more stretched, this point is called equilibrium point). This elastic force which pulls the block towards the equilibrium point is also called restoring force, which emerges to restore the position of the object towards equilibrium.
Let’s look at what happens in between. As the block approaches the equilibrium position, its displacement from that position becomes continually less, and the restoring force becomes continually less in proportion. As the restoring force decreases so, naturally does the acceleration it imparts; therefore, although the block moves more and more rapidly as it approaches the equilibrium position, the rate of gain of velocity becomes less and less. Finally, when it has reached the equilibrium position the restoring force has become zero and so has acceleration. The block can gain no more velocity and its rate of motion is at a maximum.
At the equilibrium position although the block is no longer gaining speed it is moving rapidly towards left, and it cannot remain at equilibrium position, but must move past it. Only a force can stop it once it is moving (Newton’s first law), and at equilibrium position there is no force to do so.
As it goes past the point of equilibrium to the left, however, it is displaced once more, and a restoring force comes into being again; this force produces an acceleration that serves to diminish its speed of movement (which is now in the direction opposed to the force). As the block continues to move leftward, the displacement and the restoring force continue to increase, and the speed reduces at a faster and faster rate until it reaches zero. The block is now motionless at a point of maximum leftward displacement, that is equal to the original extent of the rightward displacement.
Under the influence of the restoring force, the block moves to the right again, passes through the equilibrium position, and out to the original maximum rightward displacements. Then it goes back to the left, then back to the right, and so on. A vibratory motion.
In simple harmonic motion, it has been found that Hooke’s law (restoring force changes with the position of the object in direct proportion) holds at every stage of the movement. In all cases of simple harmonic motion, the crucial fact is that velocity changes smoothly at all times, never abruptly. We do not see sudden stops or jumps in magnitude of speed but only smooth transitions.
The period of vibration
A particular point of interest in any vibratory motion is the time it takes to move from the extreme point on one side to the extreme point on the other and back. The time taken to complete this motion (or any particular motion, for that matter) is the period of that motion.
Difference between vibratory and periodic motion
Motion about a circle or any closed curve can be viewed as made up of successive returns to an original point with each single movement about the curve; it is hence it is a periodic motion. A vibration also represents a series of returns to an original point, though by way of a forward-and-back motion rather than by motion in a closed curve, and a vibration can also be a periodic motion. For a motion to be vibratory, the back-and-forth movement is an essential feature.
Basic mathematical quantities to describe simple harmonic motion (SHM)
The type of motion, under the influence of an elastic restoring force and in the absence of all friction, is called simple harmonic motion, often abbreviated SHM.
Any sort of motion which repeats itself in equal intervals of time is called periodic, and if the motion is back and forth over the same path it is also called vibratory or oscillatory.
A complete vibration or oscillation means one round trip, say from a to b and back to a, or from o to a to a to b and back to o.
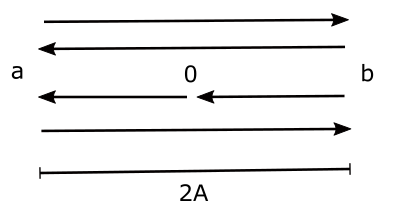
The periodic time, or simply the period of the motion, represented by T, is the time required for one complete vibration. SI unit is seconds.
The frequency f, is the number of complete vibrations per unit time. Evidently the frequency is the reciprocal of the period, or,
$f =1/T$
The SI unit of frequency is per second or 1/sec and it is called Hertz.
The displacement, x at any instant, is the distance away from the equilibrium position o or centre of the path at that instant.
The amplitude, A, is the maximum displacement from centre o, or equilibrium position. The total range of the motion is therefore 2A.
