LEARNING OBJECTIVE 3.2.A - Describe the work done on an object or system by a given force or collection of forces. AP MECHANICS -C LEARNING OBJECTIVE INT 4.A -Describe the work done on an object as the result of the scalar product between force and displacement. Explain how the work done on an object by an applied force acting on an object can be negative or zero.
Having considered the simple case of calculating Work in the last section, where the object moves along the line of action of force, now we can use some mathematics to obtain a wider and more general expression for Work.
Suppose a constant force F acts on a body, while the body gets a displacement S at angle $\theta$.
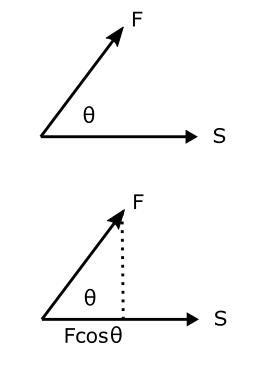
In order to calculate the work in this case first we will need to resolve the force into parallel and perpendicular components. The perpendicular component will be $FSin\theta$. As there is no displacement of the body along the perpendicular direction the Work done by this component is simply zero.
The component of the force acting along the line of displacement is $FCos\theta$ and the body gets a displacement S along the line of action of this force hence the Work:
$W = FCos\theta S$
Mathematically, For two arbitrary vectors A and B, the product of their magnitudes and the cosine of the angle between them is called the dot product (or scalar product) of the vector. A.B = $ABCos\theta$
Using the above definition we can now write our equation in vector format.
$W = \textbf{F.S} = FSCos\theta$
Where F and S are force and displacement in vector format.
Rules for evaluating vector dot product
Once we express the force and displacement in vector format. It is fairly easy to use vector algebra to find the dot product or also called scalar product.
The dot product of two vectors A and B is also equal to the sum of the products of the corresponding components of the two vectors, or
$\textbf{A.B} = A_xB_x + A_yB_y$
Using the above rule we can calculate work as follows. If the components of F along X and Y axis are $F_x$ and $F_y$ , and those of s are $\Delta x$ and $\Delta y$, then the the dot product means that the work can be written
$W = F_x\Delta x + F_y \Delta y$
Once we have the values we simply sum them arithmetically like simple numbers. Note that although this equation expresses the work as a sum of contributions from the x, and y components of the force and the displacement, the work does not have separate components. The two terms on the right are merely two terms in a sum. Work is a single-component, scalar quantity, not a vector quantity.
