LEARNING OBJECTIVE 3.2.A - Describe the work done on an object or system by a given force or collection of forces. AP MECHANICS -C LEARNING OBJECTIVE INT 4.B -Calculate a value for work done on an object from a force versus position graph.
Consider a body moving in a straight line under the influence of force F. For simplicity, we assume that displacement of the body happens in the direction of force. In this case, Work done is a simple multiple of force F and displacement $\Delta x$.
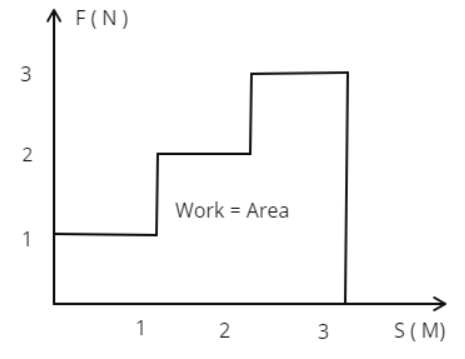
Now suppose this force varies over a period of displacement. Suppose the force is 1 N in magnitude from x = 0 to x = 1 m, this increases to 2 N from x = 1 to x = 2 m and increases to 3 N from x = 2 and X = 3 m. How much is the total work done. Clearly, we need to find the work done in three different segments and add them up arithmetically. So for the first segment F = 1 N and $\Delta x$ = 1 – 0 = 1 m, hence W = 1 $\times$ 1 = 1 J. For the second segment segment F = 2 N and $\Delta x$ = 2 – 1 = 1 m, hence W = 2 $\times$ 1 = 2 J. For the third segment F = 3 N and $\Delta x$ = 3 – 2 = 1 m, hence W = 3 $\times$ 1 = 2 J. Hence, total work done by the force F will be simply 1 J + 2 J + 3 J = 6 J. Refer to the Figure 8, you can see that this is also equal to area enclosed between the F and x axis.
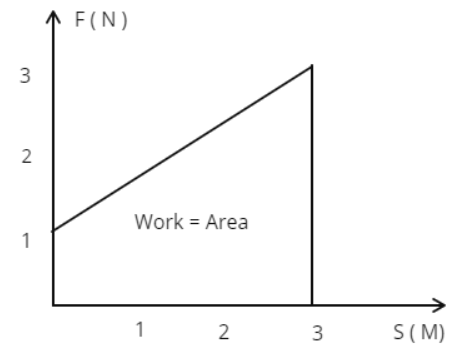
Now suppose instead of F varying discretely like the last example, it varies continuously. This means value of F varies at each and every point as a function F (x), refer Figure. Suppose the force increases linearly at x = 0 from 1 N to 3 N at X = 3 m, What will be the total work done? Obviously, it will be area enclosed between the F (x ) and the x axis. In this case it will ( 1/2 $\times$ 3 $\times$ 2 ) + ( 3 $\times 1 $) = 6 J.
We have now found a way to calculate the work done by a force from the force-displacement graph. Let’s now take a general case where the force varies as a function of x. Such a variable force can be expressed as a function of position as
$F_x = F (x)$
Now if the force varies with displacement continuously such as shown in the figure below:
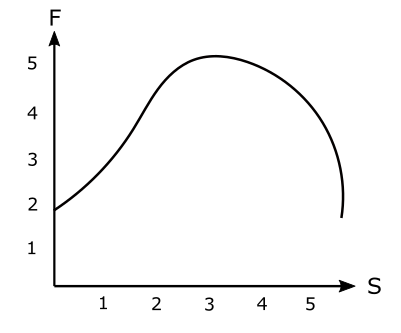
We can simply find the total work done by finding the total area under the curve.
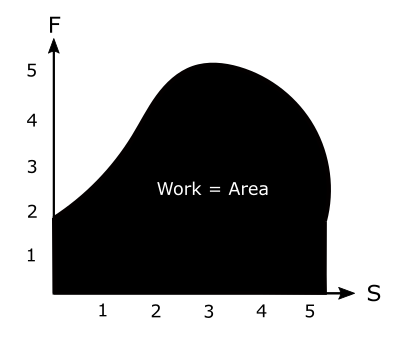
Work is area under F-S curve. Area above the axis is positive and area below the axis is negative. Total work will be equal to arithematical sum of these areas.
Work as area under curve
