LEARNING OBJECTIVE 3.A.1.1 - Express the motion of an object using narrative, mathematical, and graphical representations. AP MECHANICS -C LEARNING OBJECTIVE INT 2.C -Calculate the velocity of an object moving in a horizontal circle with a constant speed, when subject to a known centripetal force.
In a case of uniform circular motion, an object moves with constant speed v along the circumference. The velocity always remains directed towards the tangent at all points, this means the magnitude of the velocity remains constant and only its direction changes. The change in direction indicates an acceleration. Let’s try and find the direction of acceleration.
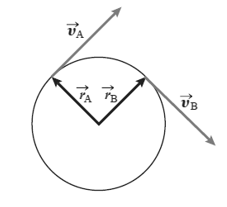
The figure shows an object moving around a circle at a constant speed. The velocity at point A is $\overrightarrow{V_A}$ and the velocity at point B is $\overrightarrow{V_B}$. Appreciate the fact that as the body is moving with constant speed the magnitude of $\overrightarrow{V_A}$ and $\overrightarrow{V_B}$ will be the same. But, during the motion from point A to point B is the direction of velocity vectors will change, hence the acceleration. The position vector at point A is $\overrightarrow{r_A}$ and B is $\overrightarrow{r_B}$, again the magnitude of these position vectors is also the same and equal to the radius r of the circle.
The definition of average acceleration is
$\overrightarrow{a_r}= \frac{\overrightarrow{\Delta v}}{\Delta t}$
It is now evident that the direction of acceleration will be in the direction of $\overrightarrow{\Delta v}$. To determine the direction of $\overrightarrow{\Delta v}$, we can redraw the position and velocity vectors using the principle that vectors can be freely moved as long as we don’t change the magnitude and direction. We can observe that $\overrightarrow{\Delta v}$ and $\overrightarrow{\Delta r}$ are perpendicular to each other. This means the acceleration in a uniform circular motion points inwards towards the centre of the circular arc.
Let’s note down this important result:
The acceleration vector in the case of uniform circular motion points to the centre of the circle. Therefore, an object moving in a circle must always accelerate towards the centre, We have a special name for this and we call it Centripetal acceleration.
What is centripetal acceleration ?
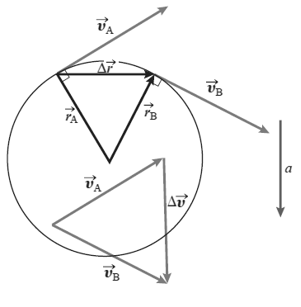
Now let’s try to compute the magnitude of this acceleration vector. In order to do that we will resort to geometry. let’s start by making two triangles. First, we can make a triangle with position vectors $\overrightarrow{r_A}$ and $\overrightarrow{r_B}$, clearly, the change in position will be the third side of the triangle represented by $\overrightarrow{\delta r}$, as shown in Figure 10. Second, we can make another triangle by moving velocity vectors $\overrightarrow{V_A}$ and $\overrightarrow{V_B}$ and the third side will represent $\overrightarrow{\Delta v}$. In these triangles angle formed between two position vectors will be the same as the angle formed between two velocity vectors as velocity vectors in a circular motion are always perpendicular to the position vectors. Further, since we are considering uniform circular motion the magnitude of velocity vectors i.e. the length of vectors will be the same, obviously length of position vectors is also the same in the first triangle as they are the radius of the circle. This allows us to use an important property of a similar triangle, the ratio of sides of similar triangles are equal. Hence for our two triangles, we can write:
$\frac{\Delta V}{v} = \frac{\Delta r}{r}$
Rearranging the above equation for $\Delta v$ and dividing both sides by $\Delta t$ we get,
$\frac{\Delta v}{\Delta t} = \frac{v \Delta r}{r \Delta t}$
For a very small value of $\Delta t$ we can say that the left side of the above equation will be our Centripetal ( Instantaneous) acceleration $ a_c $ and the ( $\Delta r / \Delta t$ ) will be equal to v. Hence we can write:
$a_c = \frac{v \times v}{r} = \frac{v^2}{r}$
We have now established both the magnitude and direction for the Centripetal acceleration of an object moving around a circle with constant speed or uniform circular motion. Figure 11 summarises our findings. The Centripetal acceleration ( name because it points to the centre of the circle which means it is centre-seeking or centripetal ) vector is perpendicular to the velocity vector and points radially inward towards the centre of the circle. The magnitude of the centripetal acceleration vectors at any point is the same and equals to ( $v^2$ /r ).
In the next section we will look at alternate ways of describing circular motion.
