LEARNING OBJECTIVE : 7.1 Describe simple harmonic motion.
In the last section, we derived kinematical equations describing simple harmonic motion as well as Newton’s law equivalent describing the relationship between restoring force and acceleration. The presence of restoring force is an essential ingredient for a body to perform simple harmonic motion.
We will now explore how to start such a motion in the first place. The very first requirement is a system where restoring forces emerge when a body is displaced from its equilibrium position. Mechanisms such as spring is one of the ways to ensure the emergence of restoring force. However, there are several other situations where restoring forces do emerge. In fact the restoring forces are likely to emerge when the body is in stable equilibrium and its potential energy profile is that of a well. Refer to the figure below. Consider the location of the object at B. If the object is displaced towards A or C restoring forces will emerge, pulling it back to stable equilibrium B. If you are not clear refer to the potential energy section.
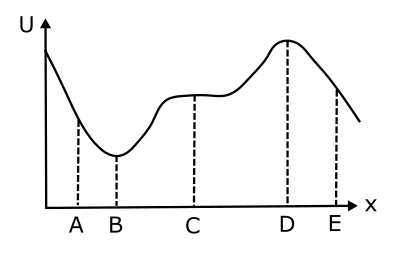
In nature apart from elastic forces sometimes gravitational, buoyancy forces can also provide the necessary role of restoring forces.
Once the object is at a stable equilibrium, for the motion to begin first we need to move the object away from the equilibrium point. This can only be done by doing some work on the system. The work done by the external agent could then become initial energy transferred to the system, hence moving the object away from its equilibrium position. Once the object moves away from the equilibrium position restoring forces will emerge and start the SHM. This initial energy could be imparted in the form of potential or kinetic energy:
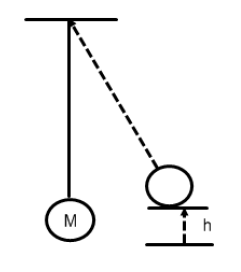
Potential energy: Consider lifting a pendulum, when we as an external agent lift the pendulum bob, we do some work against gravity, this work then gets stored as the gravitational potential energy of the pendulum. Once we release the pendulum the restoring forces start the SHM.
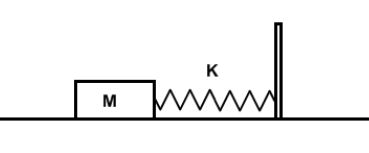
Similarly, when we compress a block against a spring we do work against the elastic forces, which eventually gets stored in the spring as elastic potential energy. When we release the block, the restoring forces start the SHM.
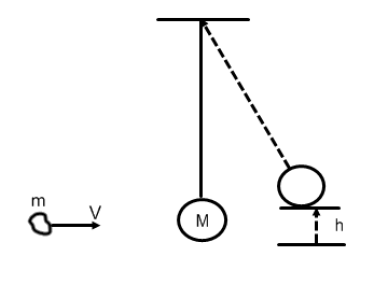
Kinetic energy: Now consider, instead of doing the work ourselves to impart potential energy to the system. We can consider an alternative way to achieve the same. If we fire a putty with some KE and it hits the bob and raises the pendulum to the same height, we can say this time we provided the initial energy by virtue of kinetic energy of the putty.
Similarly, if we fire a bullet towards the block, its KE can be used to start the SHM:
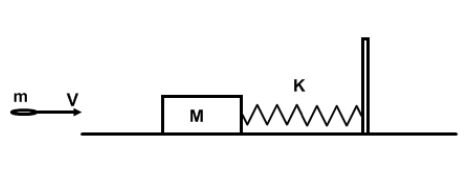
This means to start the SHM, we need two things:
- Mechanism to produce restoring force
- Initial energy to displace the body from its equilibrium position
Now as you can argue higher this initial energy, the bigger the amplitude (extreme displacement from equilibrium) will be. Hence the amplitude A can be directly computed if we know how much initial energy was provided to the system. A moment of caution though when considering KE also take into consideration whether the collision with the system is elastic or inelastic. In case of inelastic collision, some of the energy of the agent will be destroyed and useful energy imparted to the system will be less.
