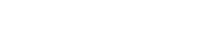LEARNING OBJECTIVE 3.A.1.1 - Express the motion of an object using narrative, mathematical, and graphical representations. AP MECHANICS -C LEARNING OBJECTIVE INT 2.C -Describe the direction of the velocity and acceleration vector for an object moving in two dimensions, circular motion
One of the most interesting applications of Newton’s Law is to solve problems related to the motion of an object moving in a circle. Many such practical examples can be encountered such as your car taking a turn on a roundabout, a satellite moving around earth and so on. In this chapter, we will see how we can apply our knowledge of kinematical quantities such as velocity and acceleration along with Newton’s law to understand and solve problems related to uniform circular motion.
What is a uniform circular motion?
Consider an object moving in a circle. Suppose it takes time T seconds to complete one full rotation. If the object keeps rotating and completes its second rotation again at the same time T, we can say that the object is not gaining any speed during rotation and moving with constant speed. Hence it takes the same time T to complete one full rotation. Such a motion in a circle where the object’s speed remains constant or uniform is called Uniform Circular Motion.
Measuring and describing circular motion
If we hope to understand and quantify the uniform circular motion we will surely need to first define and measure a few relevant variables, which can describe such a motion. For example, when we were dealing with motion in a straight line we defined displacement ( a measure of how much the position of an object changed ), velocity ( how fast or slow an object is moving ) and acceleration ( how fast or slow the velocity is changing ). So what is the equivalent of displacement, velocity and acceleration in the case of uniform circular motion?
Displacement in a uniform circular motion: Angular displacement
Consider a rectangular object that rotates by an angle around an axis. The rotation of an object can then be described very simply by specifying the angle of rotation.
So far we have used Newton’s law to handle the motion of an object moving in a straight line, but when an object rotates through an angle, the linear motion of its particles is quite complex because different particles in the objects get displaced by different amount and direction. Refer to Figure 6 and observe the displacement of points A, B and C.
To deal with the rotational motion such as this we must, therefore, describe motion in terms of angles – and also express laws of motions and Kinematical quantities in terms of angles.
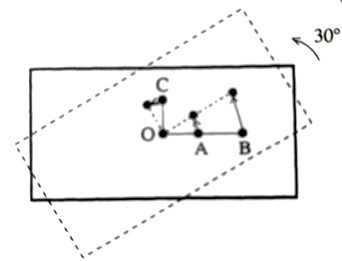
Let’s first start by fixing the angular position. Refer to Figure below if the rod rotates in a counter-clockwise direction, we can then measure the angle it makes from some standard orientation (the equivalent of origin in linear ) and specify the object’s angular position by $\phi$.
For example, the successive angular positions could be $\phi_1$ = $30^{\circ}$ and $\phi_2$ = 60$^{\circ}$ both counter-clockwise. We have used the dashed line as a fixed orientation.
Now having two positions in hand we can compute Angular displacement as
$\Delta\phi = \phi_2 -\phi_1 $
So angular displacement in our example will be 60$^{\circ}$ – 30$^{\circ}$ = 30$^{\circ}$, counter-clockwise.
Nice and easy, now consider an object rotating through half a circle we can then describe its angular displacement as 180$^{\circ}$ counter-clockwise, if it completes one full circle we will say 360$^{\circ}$ counter-clockwise, what will happen if the object starts taking more than one rotation? We can practically measure degrees up to 360$^{\circ}$, and that can limit our analysis.
In order to handle such cases it is convenient to specify an angle as a pure number, which can start at zero and can go up to $+-\infty$
Why we need radian
Radian as a measure of angular displacement
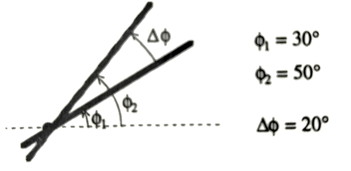
Consider a circle with a radius r by geometry we know that the circumference of the circle is $2\pi r$. Refer to the figure and note that the arc AB is of length s and it varies as the angle $\theta$ increases. At $\theta = $ 0$^{\circ}$, $s=0$, at $\theta =$ 90$^{\circ}$, $s=(2\pi r / 4)$ , at $\theta =$180$^{\circ}$, $s=(2\pi r / 2)$ and at $\theta =$360$^{\circ}$, $s=(2\pi r)$, which means we have a way of relating the angle with a linear variable distance.
Now if we look carefully the issue is that the value of s in this case depends upon r, so we will end up getting different values of s for different circles ( Refer to Figure above). Now if we divide the length s with the radius we obtain a pure number s/r which is now independent of the radius of the circle under consideration. As you can imagine the value of s will start from zero and increase as we move along the circumference whereas the value of r will be fixed for the circle under consideration, as the s will increase the value of s/r will also increase and at some point s will be equal to r and the value of s/r will become equal to 1, i.e when s=r. We define this as one Radian. In a circle, $s=2\pi r$ and s/r = $2\pi$. Now we can simply deduce number of degrees in a radian. In a cirlce we have $2\pi$ radians, which in case of degrees is $360^{\circ}$ so we can write
$2\pi = 360^{\circ}$
Solving this we can say 1 Radian = 57$^{\circ}$ (approximately). All we have to notice is that we have now converted our degree measure into a pure number measure called Radian, allowing us to measure angular displacement. If an object moves a complete circle we say it has covered an angular displacement of $2\pi$ radians, which indeed is a number $2 \times (22/7) = 6.28$ radians. If the object moves along the circle twice we say it has covered an angular displacement of $2 \times 6.28 = 12.56$ radians and so forth.
Velocity in a circular motion: Angular velocity
Once we have defined angular displacement as $\Delta\phi$ , which we are going to measure in radians, it is easier to see how we can define Angular velocity. By using the fundamental definition of velocity as rate of change of displacement we say if it took $\Delta t$ time for an object to cover an angular displacement of $\Delta\phi$, the angular velocity will be simply:
$\omega = \frac{\Delta\phi}{\Delta t}$
Acceleration in a circular motion: Angular acceleration
Once we have angular velocity defined as $\omega$ we can now go ahead and define the change in the angular velocity as $\Delta\omega$ and if it took $\Delta t$ we define Angular acceleration as:
$\alpha = \frac{\Delta\omega}{\Delta t}$
In the next section we will look at the centripetal acceleration