LEARNING OBJECTIVE: 7. 3 Describe the displacement, velocity, and acceleration of an object exhibiting SHM.
In Physics we study the motion of a body using equations. If the motion can be described using equations, we can accurately predict the position, velocity and acceleration of the body at a given time. When we studied linear motion or the motion of a body moving in a straight line with constant acceleration, we devised three equations which described the motion of the body. Namely,
$V = U + at $
$S = Ut + at^2 /2 $
$V^2 = U^2 + 2aS $
Let’s try to find equations which can describe SHM.
Consider, a body performing simple harmonic motion around an equilibrium point O between extremes I and II as shown in the figure. Clearly, the distance between O and point I as well as O and point II is Amplitude A.
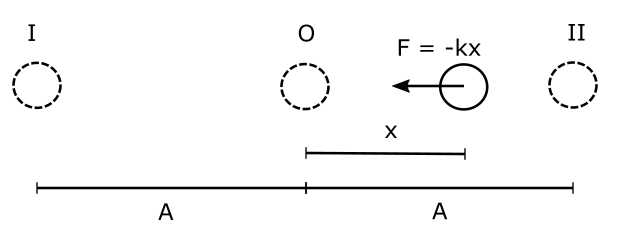
Let’s focus on the body when it is at a distance x towards right from O. At this location the restoring force will be directly proportional to the displacement and will act towards left. If we consider the right as positive and left as negative this restoring force F can be written in the form of an equation, where k is a constant, known as spring constant:
$F = -kx$
From Newton’s second law F = ma,
We can get an equation describing the acceleration of the body as:
$a = – (k/m) x$
Where m is the mass of the body.
Since k and m are constants the ratio k/m is also a constant. Hence, the acceleration is directly proportional to the displacement from the equilibrium position. The minus sign in the equation specifies the direction of acceleration to be opposite of the displacement. That is to say, when the body is towards right of the equilibrium point the acceleration points to the left and when the body is towards left of the equilibrium point the acceleration is towards right.
Hence, we conclude whenever a body is in periodic motion such that its acceleration is directly proportional to its displacement from the equilibrium position the motion is SHM. Alternatively, if the ratio of acceleration and displacement of the body doing periodic motion ( k/m) is constant, the body is said to be performing simple harmonic motion.
How about the velocity of the body? Surely when the body is at the extremes it turns around, this means its velocity is zero at the extremes. Secondly, when the body is at the equilibrium point its acceleration becomes zero and reverses its direction hence, the velocity is maximum at the equilibrium point.
Having developed a qualitative description of simple harmonic motion, that is describing force, acceleration and velocity, let’s now develop a mathematical model for the same. The only trouble is that we are dealing with force which is variable in nature and hence the mathematics to deal with such motion is complex and involves calculus.
One therefore searches for ways to represent this SHM with some other motion where the acceleration has a constant magnitude. If we are able to find such a representation, we can avoid complex mathematics.
One of the closest motions which is periodic, is a uniform circular motion and we have developed a complete model of circular motion using variables such as period, frequency, linear and angular velocity. Just to recall here are the equations which describe the motion of a body doing uniform circular motion with radius R.
$ V = \omega R $
$T = 2\pi R /V $
$T = 2\pi / \omega$
$f = 1/T $
Where $\omega$ is the angular velocity, V is linear velocity, T is the period of motion and f is the frequency.
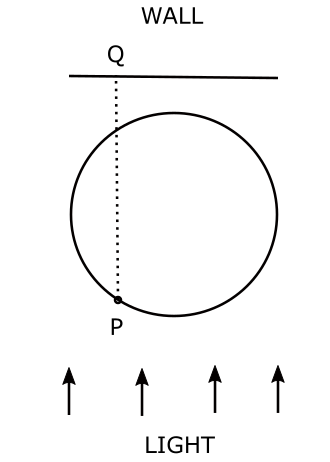
Let’s now consider the below experiment. Suppose a body is performing a uniform circular motion. We place a light source which projects the motion body moving in a circle on a wall. For example, when the boxy is at point P, rotating clockwise we can see its shadow on the wall at point Q.
When the body rotates in a circle, we will find that what we see in the shadow is the back-and-forth motion of the shadow along a straight line on the wall. This back-and-forth straight line is in sync with the uniform circular motion the object is performing. Clearly, the extremes of this motion will be apart by the diameter of the circle. Hence the amplitude of this straight-line motion will be the same as the radius of the circle.
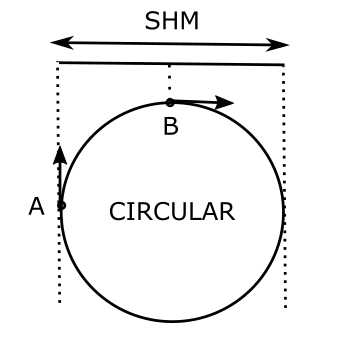
Consider the situation when the body doing circular motion will be at one of its extremes, at point A (right or left), at that point its linear velocity will be perpendicular to the radius of the circle hence the shadow which moves left and right along the wall will have zero velocity, horizontally. Having zero velocity at the extremes is one of the characteristics of SHM.
Now consider, when the circulating body is at point B, which is directly above its centre. At this point, the linear velocity will be parallel to the horizontal shadow. That is to say, the velocity of shadow will vary between the point A projection (will be zero) to that of the point B projection (will be maximum and equal to the linear velocity of the circular motion). Having maximum velocity at the equilibrium point is another characteristic of a SHM.
The shadow moving in a periodic motion is also moving in a simple harmonic motion, with the same period as the body doing the circular motion. The amplitude of this SHM is equal to the radius of the circle.
Let’s now formalize this using some basic math.

Consider a body moving in a uniform circular motion with a constant linear speed V. Let the radius of the circle be A. If we consider the projection of this body along the diameter with positions I and II , the body will be equivalently doing SHM along this diameter with an amplitude equal to the radius A. Points I and II are the extremes of this SHM and centre of the circle O will be the equilibrium point. Let’s now recall the basic variables of uniform circular motion. The angular speed $\omega$ will be related to linear speed V as
$V = \omega R$
Now consider a point P on the circumference of the circle. Its projection on the diameter will be at point Q. This point Q will be at a distance x from O.
Where $x = A Cos \theta$
Now we can ask, what will be the velocity of the object performing SHM along the diameter at a distance x from equilibrium point O? As it is the case the answer is very simple. The linear velocity of the body doing the circular motion is V and it is tangent to point P. If the angle POQ is $\theta$ then the projection of this linear velocity V along the x-axis will be:
$-V Sin \theta$
Where $\theta$ is in radians. The minus sign signifies the direction of velocity opposite to the displacement x. Let’s now calculate the acceleration. The radial acceleration of the body moving in a circle is of magnitude $V^2/A$ and always points towards the centre. Hence, its projection on the X-axis will be:
$a = – (V^2/A) Cos \theta $
In the equations derived above the angle $\theta$ is called phase angle or simply phase. If the starting point of the SHM is taken at point II at time t = 0 then clearly with angular velocity $\omega$, we can connect time t with $\theta$ as,
$\theta = \omega t $
Allowing us to transform our equation for displacement x as a function of time t:
$X(t) = A Cos\theta = A Cos \omega t$
We can now go a step further and say as
$\omega = 2\pi / T=2 \pi f $
The displacement when expressed in terms of frequency f and time t will take the form:
$ X(t) = A Cos( 2 \pi f t ) $
Note: Like we had the equation: $S = ut+ 1/2 at^2$
For calculating the displacement in the case when the body was moving in a straight line with constant acceleration. We now have an equation for calculating the displacement of a body performing SHM.
Let’s now transform our Velocity equation.
$V(x) = – V Sin \theta$
Since $V = 2 \pi / T = 2 \pi f$, we can write:
$V(t) = -2 \pi f A Sin (2 \pi f t ) $
And this will be equivalent to V = u + at for the motion with constant acceleration.
Since :
$Cos\theta = \frac{x}{A}$ and $Sin\theta = \sqrt {1- cos^2 \theta} = \sqrt {1- (\frac{x}{A})^2 } $, we can now transform the velocity equation:
$V(t) = \pm 2 \pi f A \sqrt {1- (\frac{x}{A})^2 } $ or
$V(t) = \pm 2 \pi f \sqrt{A^2 – x^2}$
The plus-minus sign is required because the body at a particular value of x will have two equal but opposite velocities when moving from left to right and then from right to left.
This equation connects the velocity of the body with its location by eliminating time from the equation hence straight line motion with constant acceleration is equivalent to $V^2=U^2+2aS$, but for SHM.
Finally, the Acceleration of the body doing SHM will be:
$a (t ) = – 4 \pi^2f^2A Cos (2 \pi ft) $
Since $ A Cos (2 \pi ft) = x / A $
$a(t) = – 4 \pi^2f^2 x $
