LEARNING OBJECTIVE 3.3.A - Describe the potential energy of a system. AP MECHANICS -C LEARNING OBJECTIVE CON 1.D -Derive the expression for the potential energy function of an ideal spring.
In the last section, we derived an expression to calculate the numerical value of kinetic energy. Let’s now derive expressions for potential energy associated with two of the forces we will be frequently dealing with; namely gravitational and elastic forces.
In order to derive such an expression we will use the following procedure. First, we will assume that the body moves from point A to B very slowly such that its initial and final kinetic energy is zero. This will allow us to arrive at calculations easily. In the absence of a change in the kinetic energy of the object during motion from A to B, all the work done by the forces so involved will get stored as potential energy.
A spring is a simple and closest representation of elastic forces emerging in bodies in case of deformation. Let’s use the spring to find an expression for elastic potential energy. We will use the exact same process we used in the last section.
Suppose the spring is in an undeformed state and we apply a force F of variable magnitude which adjusts with the emerging elastic force but just a bit more than the elastic force so that we continue to stretch the spring by a distance d as shown in the figure.
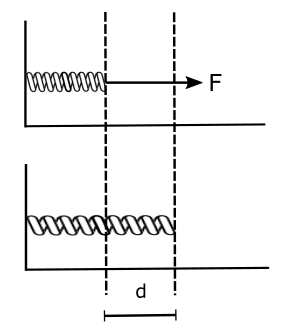
How much work the force F do stretching the spring by distance d? Given the displacement is in the direction of the force F, it will be equal to Fd, the only issue is that F is a variable force which varies with x itself. Hence we will need to calculate a differential work done by the force when it is stretched by x already and further stretches the spring by dx. Once we have this differential work, we simply need to sum it from x = 0 to x = d. Consider the spring stretched by x, at this position the force F(x) = kx, where k is the spring constant of the spring. This force now works to stretch the spring by a small amount dx. Hence the differential work done will be dW = F(x) dx = kx dx. In order to find the total work done we will now need to sum up all such differential work from x = o to x = d, the simple way of doing it is by integration hence,
$ W = \int dW = \int_0^d kxdx = \frac{kd^2}{2} = PE $
Given there is no change in the kinetic energy of the spring, all this work is stored as the potential energy of the spring. Hence generalizing we can say the following:
The potential energy stored in an elastic spring of spring constant k, when stretched by a distance x is equal to
Elastic potential energy of a spring
$\frac{kx^2}{2}$
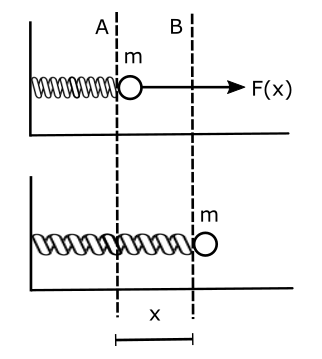
Let’s expand our spring system in the last example with a ball of mass m, as shown in Figure below. If again we stretch the spring by a distance x such that there is no change in KE of the system, we can say that energy stored in the spring will be: $kx^2/2$. When the force is removed the ball will start to move towards the left, the spring will now start losing the PE which eventually will be gained by the ball as KE such that KE + PE = constant at all times.
The figure below shows the energy diagram for such a system.
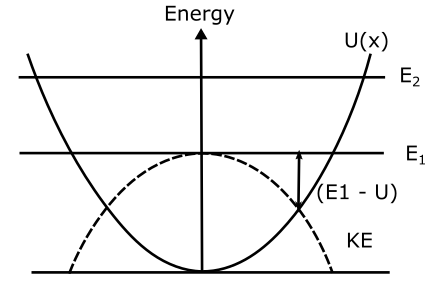
Notice the U(x) curve which plots the potential energy of the spring with varying values of x, given the U(x) this time is given by $kx^2/2$, a quadratic dependence the curve is a parabola, symmetrical about x = 0, values of negative x means compression of the spring whereas positive x means elongation of the spring. Suppose while stretching the spring with an external force we have done $E_1$ work. The energy stored in the spring is also $E_1$. This is shown by a line parallel to the x-axis and this shows the maximum value of U(x). At this level, KE = 0 and PE will be the maximum. At any intermediate point between x = 0 and x, the kinetic energy can be found by measuring the distance of the U(x) curve from the line $E_1$ as KE = $E_1 – U (x) $, in agreement with the law of conservation of mechanical energy, because KE + PE remains constant throughout the motion for any value of x.
