Calculating gravitational potential energy

LEARNING OBJECTIVE 3.3.A - Describe the potential energy of a system.
AP MECHANICS -C LEARNING OBJECTIVE CON 1.E -Calculate the potential energy of a system consisting of an object in a uniform gravitational field.

In the last section, we derived an expression to calculate the numerical value of kinetic energy. Let’s now derive expressions for potential energy associated with two of the forces we will be frequently dealing with; namely gravitational and elastic forces.

In order to derive such an expression we will use the following procedure. First, we will assume that the body moves from point A to B very slowly such that its initial and final kinetic energy is zero. This will allow us to arrive at calculations easily. In the absence of a change in the kinetic energy of the object during motion from A to B, all the work done by the forces so involved will get stored as potential energy.

Suppose we move a body from point A to point B near the surface of the earth. Let the height of point A be $h_1$ and B be $h_2$, given $h_2 > h_1 $. Assuming there is no change in the kinetic energy between A and B, as we move the ball very slowly then all the work done by us will be stored as potential energy or more specifically in this case gravitational potential energy.

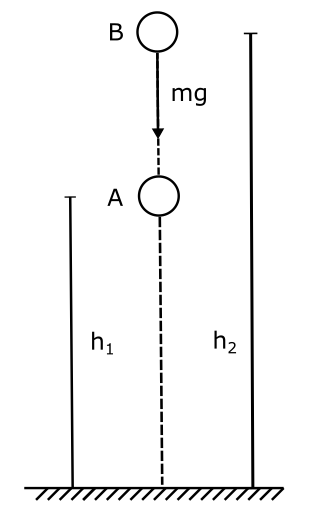
During the motion of the body from A to B, the force of gravity acting on the body is mg ( downwards), where m is the mass of the body and g is the acceleration due to gravity. In order to move the body we will have to counter this force such that the body moves with constant velocity. Hence the force we need to apply will be equal to mg.

This force will move the body from A to B doing work and the work done will be simply ( $mg \times displacement $), how much is the displacement from A to B, it is clearly $ ( h_2 – h_1 )$, hence the work done by us will be:

$W_g = mg ( h_2 – h_1 ) = U_g $

This work will be equal to the gain in the gravitational potential energy.

You may be wondering what will happen if we measure the height not from the earth but from some other place, such as from a table of height s. In any such cases, you will also notice that in the final expression for the gravitational potential energy, what matters is not the absolute value of $h_1 \mbox{ and } h_2 $, but the difference $ ( h_2 – h_1 ) $. Hence the choice of reference line from where we measure these heights is immaterial. If you are still not convinced let me do simple arithmetic to show you why. Suppose we choose our reference point for measuring the height $ h_1 \mbox{ and } h_2 $ from a table of height s.

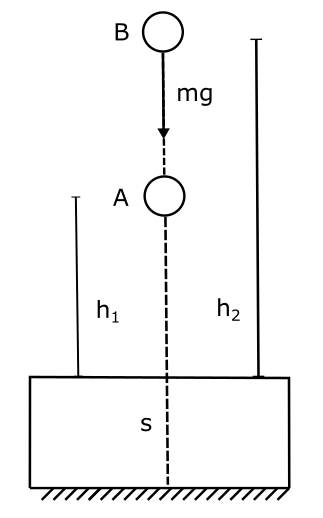
The initial height of both $h_1$ and $h_2 $ will simply reduce by an amount s to $h_1 -s$ and $h_2 – s$ compared with the last case. But, there will not be any difference in $h_2-h_1$ ( as +s and -s are equal to zero). Hence we conclude.

Change in gravitational potential energy, when an object moves through a vertical height H along any path, is given by mgH, where H = [ $h_{\mbox{final height}} – h_{\mbox{initial height}}$ ]. \ Unlike kinetic energy which cannot be negative, gravitational potential energy could take negative, zero or positive values depending upon the reference level.

Calculating gravitaional potential energy

Let’s take a moment to analyse what the expression for the gravitational potential energy means. The expression mgH means that if H = 0, that is when the object is at the level of our reference line $U_g = 0$. As the value of H increases $U_g$ increases in direct proportion to H as m and g are constant.

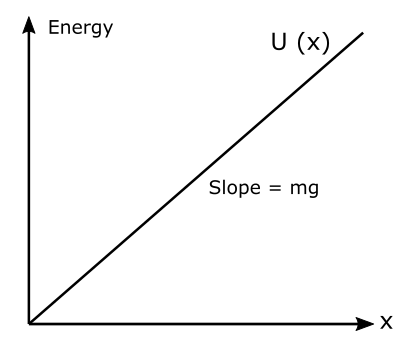
If we use x as a general notation instead of H, we can now write U(x) = mgx. We can also graph this function. This graph will pass through the origin and increase with x with slope mg. Ref to Figure 14.

Clearly, the U(x) could take negative, zero or positive values depending upon the choice of our reference line or datum. But what will be the maximum value it can take? Going back to where this potential energy originates – we know that it originates from external work. If we raise a body to height x we have to do some work against the gravitational forces. This work then gets stored as potential energy. Hence the maximum value of the U(x) is the value of ME or mechanical energy. Assuming all the work done by us is stored in the form of potential energy only and there is no change in the KE then W = ME = U(x), the maximum value. Let’s now mark this maximum value of U(x) on the graph, with a horizontal line parallel to the x-axis.

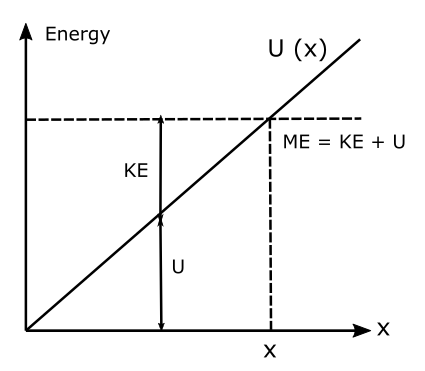
If we now choose any point between the zero and maximum value of U(x), the distance from the x-axis will represent the value of potential energy the object has at that particular point and the distance from the ME line to the point will represent the KE the object has any point. Clearly, when the PE is zero the total ME is only KE and when the U (x)= ME, the KE is zero. At all points the value of KE + U remains constant. This kind of graph is called an energy diagram and is a useful tool for analysing various physical systems.