Law of conservation of energy

LEARNING OBJECTIVE 3.4.C - Describe how the selection of a system determines whether the energy of that system changes.
AP MECHANICS -C LEARNING OBJECTIVE CON 2.A -. Describe physical situations in which mechanical energy of an object in a system is converted to other forms of energy in the system.

An object thrown into the air with a certain kinetic energy returns to the ground without quite the original kinetic energy. A small quantity has been lost through air resistance. Again, if an elastic object is dropped from a given height, it should (if mechanical energy is to be truly conserved) bounce and return to exactly its original height. This it does not do. It always returns to somewhat less than the original height, and if allowed to drop again and bounce and drop again and bounce, it will reach lower and lower heights until it no longer bounces at all. So where is the kinetic energy of the ball disappearing if not stored as a gravitational potential energy?

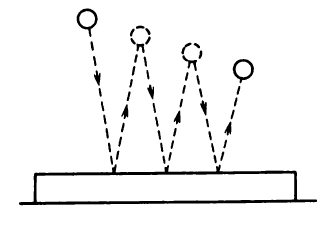
This can be explained if we consider frictional forces. The resistance of the air in which the ball moves and the internal friction between the materials of the ball and the slab.

In general, in the presence of friction, the law of conservation of mechanical energy is always violated, and the total energy of bodies decreases. The work against friction is done at the expense of this decrease in energy.

A closer analysis reveals that it is not only the air resistance that interferes but also the imperfect elasticity of the body itself. Indeed, if a lump of soft clay is dropped on a floor, its potential energy is converted to kinetic energy, but at the moment it strikes the ground all its kinetic energy is gone—and without any re-formation of potential energy. The mechanical energy disappears in these cases.

All motions in nature (with the exception of motions in vacuum, like the motion of celestial bodies) are accompanied by friction. Therefore, for these motions the law of mechanical energy conservation is violated, this violation being always such that the total mechanical energy decreases.

Unfortunately, the “law of conservation of mechanical energy,” however neat it might seem under certain limited circumstances, has its imperfections. The existence of imperfections in nature such as air resistance, friction and imperfect elasticity throws the law of conservation of mechanical energy as a true conservation law. Hence, the need for a new law.

If we seek a conservation law that will involve work, we must make up our minds that for every loss of mechanical energy, there must be a gain of something else. That something
else is not difficult to find. Friction, one of the most prominent imperfections of the environment, will give rise to heat, and if the friction is considerable, the heat developed is likewise considerable. For example, the temperature of a match-head can be brought to the ignition point in a second by rubbing it against a rough surface.

Conversely, it is possible to convert heat into mechanical energy. The heat of the sun raises countless tons of water vapour kilometres high into the air so that all the mechanical energy of falling water (whether rain, waterfalls or flowing rivers) originates from the sun’s heat.

It seemed clear, therefore, that one must add the phenomenon of heat to that of work, kinetic energy and potential energy, in working out a true conservation law. Heat, in short, would have to be considered another form of energy.

Heat as a form of energy

But if that is so, then any other phenomenon that could give rise to heat would also have to be considered a form of energy. An electric current can heat a wire and a magnet can give rise to an electric current, so both electricity and magnetism are forms of energy. Light and sound are also forms of energy, and so on.

If the conservation law is to include work and all forms of energy (not mechanical energy alone), then it had to be shown that one form of energy could be converted into another. In other words, in such energy conversions, all energy must be accounted for; no energy must be completely lost in the process, and no energy created.

Over a period of years in the 1840s an Englishman named James Prescott Joule (1818-1889), whose hobby was physics tested these ideas extensively. He measured the heat
produced by an electric current, heat generated by friction, heat generated by turning paddle wheels in water and so on. In doing so, he found that “a fixed amount of one kind of energy was converted into a fixed amount of another kind of energy and that if the energy in all its varieties was considered, no energy was either lost or created”. It is in his honour that the unit of work and energy in the MKS system is named the “joule.”

Now, it was natural to modify the law of conservation of mechanical energy to the law of conservation of energy.

Energy includes work, mechanical energy, heat, and everything else that could be converted into heat. Energy cannot be created nor destroyed.

Law of conservation of energy

The law was first explicitly stated in a form clear enough to win acceptance by the scientific community in 1847 by the German physicist and biologist Hermann von Helmholtz (1821-1894). It is to be noted that before Joule performed his experiments, a German physicist named Julius Robert von Mayer( 1814-1878) also believed in the law of energy conservation. Three of them, Joules, Mayer and Helmholtz are credited to discovered this law.

The law of conservation of energy is probably the most fundamental of all the natural laws. It holds for living systems as well as nonliving ones; and for the tiny world of the subatomic realm as well as for the cosmic world of the galaxies. At least twice in the last century phenomena were discovered which seemed to violate the law, but both times physicists were able to save matter by broadening the interpretation of energy.

In 1905, Albert Einstein showed that mass itself was a form of energy; and in 1931, the Austrian physicist Wolfgang Pauli (1900-1958) advanced the concept of a new kind of subatomic particle, the neutrino, to account for apparent departures from the law of conservation of energy. The nuclear bomb, for instance, is a phenomenon that can only be explained by the Einsteinian concept that mass is a form of energy.

$ E = mc^2 $

Where E stands for energy, m is mass and c is the velocity of light. No violation of the law of conservation of energy has been observed or proved yet.