Mathematics of mechanical energy conservation

LEARNING OBJECTIVE 3.4.B - Describe the behavior of a system using conservation of mechanical energy principles.
AP MECHANICS -C LEARNING OBJECTIVE CON 2.B -. Describe kinetic energy, potential energy, and total energy in relation to time (or position) for a “conservative” mechanical system.

In the last section, we introduced a very profound idea of the conservation of mechanical energy.

Let’s now shift gears and introduce some mathematics to quantify the idea of mechanical energy and its conservation.

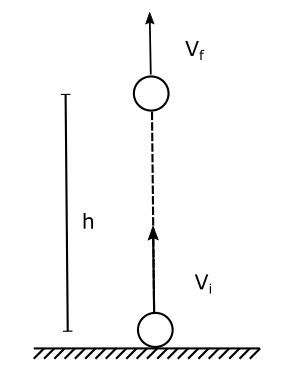
Let’s consider a ball of mass m projected vertically upward with an initial velocity $V_i$. When the body reaches the height h, let’s say its velocity decreases to $V_f$. If acceleration due to gravity is g downwards, using standard kinematics:

$V_f^2=V_i^2–2gh$

Now let’s do a small trick and divide the whole expression by m/2.

We will get:

$\frac{m{V}_f^2}{2}=\frac{m{V}_i^2}{2}–mgh$

Rearranging this we will get:

$\frac{m{V}_f^2}{2}+mgh=\frac{m{V}_i^2}{2}$

As the ball rises from the point of projection v decreases and h increases, both terms on the left side of the equation change but their sum remains constant and equal to initial kinetic energy $m{V}_i^2/2$, in line with the law of conservation of mechanical energy. All the initial kinetic energy imparted to the ball converts to final kinetic energy $m{V}_f^2/2$. The second term mgh has to be the gravitational potential energy. The total mechanical energy of the body at all points of its path is constant and equal to the initial kinetic energy.

Extending the idea with projectile motion

The law of conservation of energy is not restricted to the vertical motion. Let’s now consider a projectile launched with a velocity $V_i$ at an angle $\theta$ from the horizontal. Let the horizontal and vertical projection of this velocity be $V_{ix}$ and $V_{iy}$ respectively.

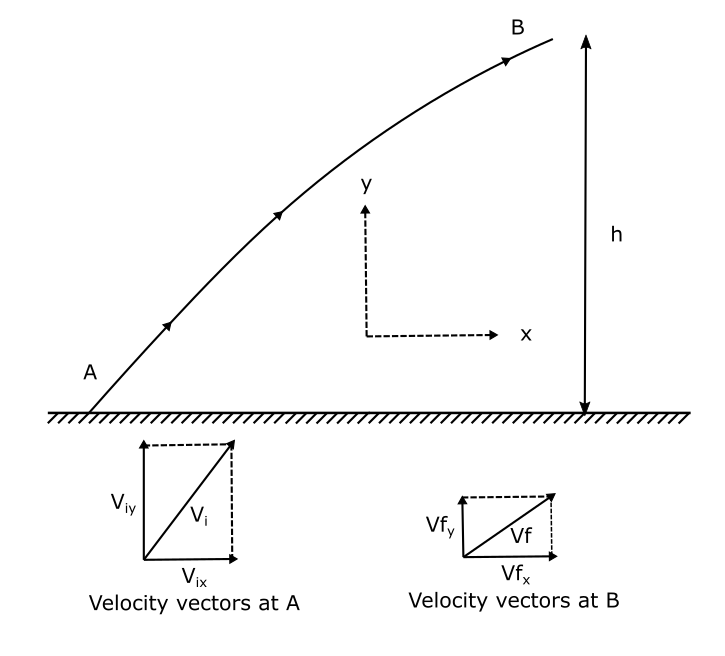
Again after the projectile travelled to a height of h, let’s say its horizontal velocity and vertical velocity is $V_{fx}$ and $V_{fy}$ respectively. Now writing the kinematical equation for both horizontal and vertical directions we will get.

For horizontal direction, there is no acceleration, hence there will not be any change in the horizontal velocity.

$V_{fx}^2=V_{ix}^2–0=V_{fx}^2$

For the vertical direction:

$V_{fy}^2=V_{iy}^2–2gh$

Again, multiplying both the equation by m/2 and then adding:

$\frac{m}{2}(V_{fx}^2+V_{fy}^2)=\frac{m}{2}(V_{ix}^2+V_{iy}^2)–mgh$

Substituting $V_f^2=V_{fx}^2+V_{fy}^2$ and $V_{ix}^2+V_{iy}^2=V_i^2$, we will get:

$\frac{m{V}_f^2}{2}=\frac{m{V}_i^2}{2}–mgh$

and finally rearranging we get:

$\frac{m{V}_f^2}{2}+mgh=\frac{m{V}_i^2}{2}$

Exactly the same expression as the case of vertical motion. The sum of the kinetic and potential energy remains constant and equal to the original kinetic energy of the projectile. So what is the difference between the two motions? Well, apart from different trajectories there are none. The final kinetic energy of the object at height h is the same hence the velocity. As the expression for the potential energy only contains height it doesn’t matter which trajectory the body takes to arrive at height h, the change in potential energy and kinetic energy remains the same. This a hint that changes in potential energy are independent of the path but only the endpoint. In this case the height. We will explore this idea further in later sections.