Understanding Work

LEARNING OBJECTIVE 3.2.A - Describe the work done on an object or system by a given force or collection of forces.

So far we have handled mechanics problems using force and Newton’s law. Now it’s time to switch to another method of analysing mechanics problems, namely the work and energy method. This method is often easier to use and can provide quick and neat solutions to mechanics problems if certain conditions are met. In this chapter, we will try to understand what is work, energy and power and how to calculate their numerical values in different scenarios.

What is work?

If you ask someone who is not a physics student – what is work? You may get different answers such as we need to work to get money. We need to work to get marks in the exam and so on. If you ask Maths students what is work, they might simply give you a formula
to calculate its value, Work = Force X Displacement. Advanced maths students may even offer formulas in vector and calculus form

$Work = W= \int F. ds$

Nice. But what exactly do we mean by work as a physical quantity and why it matters? In order to understand this we will need to travel 2300 years back in time to Greece and meet Archimedes. So let’s begin our Journey.

We will first look at the idea of the lever which Greeks used to build enormous buildings. This idea is what drives simple machines and will also help us understand what the work is.

Golden rule of mechanics

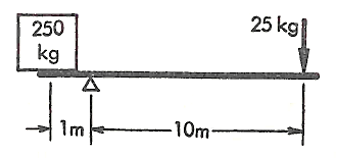
Suppose someone asked you to lift a box of mass 250 kg. You know that you simply cannot do it directly, it’s too heavy to be lifted by an average human. So you employ a trick called a lever. This simple machine allows you to perform the lifting of the box at 1/10th of the effort required in case of direct lifting. Figure 1 illustrates such a lever. Basically, you apply a 25 kg equivalent of force on one side of the lever and it allows you to lift 250 kg equivalent of weight on the other side.

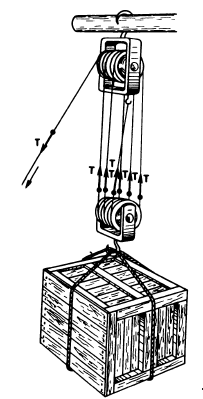
Another way of lifting the box could be using a pulley system. As there are six ropes now pulling the box up, you actually need to pull with 1/6th of the effort required in case of direct lifting.

In both cases, the advantage is that the effort you put in multiplies by a factor and is transmitted to the receiving end. In the case of the lever, you apply your effort on the right side, the lever as a machine takes that effort multiplies it ten times and transmits the same to the left side where the box is, allowing you to lift the box easily.

In the case of the pulley system, you apply your effort in terms of pull, which generates tension T in the string and then the system multiplies it six times and takes it to the load, allowing you to lift the load easily.

Going back to the origin of this rule, it appears that humans discovered this trick or rule centuries ago. But, it was Archimedes who studied it in detail and mathematically established it around 200 B.C.

This trick is also called Golden rule of mechanics.

Golden rule of mechanics

A simple machine

Any device that transfers a force from the point of application to another point where it is used, is a machine. The lever does this since a force applied on one side of the fulcrum can lift a weight on the other side; it does this in so uncomplicated way that it cannot be further simplified. It is therefore an example of a simple machine.

Other examples of simple machines are the inclined plane, wheel and axle, pulley, wedge, and screw. Virtually all the more complicated machines designed and used by mankind until recent times have been merely ingenious combinations of two or more of these simple machines.

How does a simple machine work?

A machine not only transfers a force, it can often be used to multiply that force, as in the example of the lever described above. Yet this multiplication of force should be approached with suspicion. How can one newton of force do the work of ten newtons just by transmitting
it through a rigid bar? Such generosity on the part of the universe is too much to expect. Something else must be lost to make up for it.

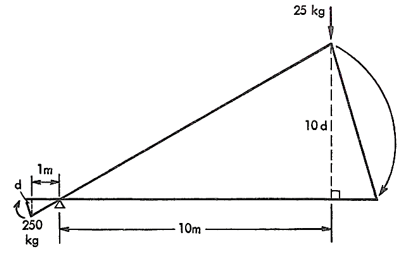
If we consider the lever lifting the 250-kilogram weight by use of a force equivalent to only 25 kilograms of weight, we can see in the Figure, that if we apply a force at a point ten times as far from the fulcrum, as the weight is, then to lift the weight a given distance, we must push down through a distance ten times as great. There is the answer! In lifting a weight by means of a lever, we may adjust distances from the fulcrum in such a way as to make use of a fraction of the force that would be required without the lever, but we must then apply that fractional force through a correspondingly greater distance. The product of the force multiplied by the distance remains the same at either end of the lever.

Mathematically,

$Force \times Distance = Constant$

This turns out to be true of any machine that seems to multiply a force. The smaller force performs the task that would require a larger force without the machine, but always at the cost of having to be exerted through a correspondingly longer distance.

This product as a physical quantity seems special and deserves to have its own name. The product of force and distance in the direction of the force is called work and is usually symbolized as W, so that

$W = F S$

If we compare two sides of the lever let’s say the forces are $F_1$ and $F_2$ respectively and distances travelled are $S_1$ and $S_2$ respectively, we can write:

$\frac{F_1}{S_2} = \frac{F_2}{S_1} \mbox{ or } F_1S_1 = F_2S_2$

The physical quantity Work W is a vector or scalar?

Since force is a vector quantity, it might seem that Work, which is after all the product of a force and a distance, might also be a vector and that one might speak of a given amount of work to the right and the same amount of work to the left as being equal and opposite. When we consider the units of work, we find that this is not the case.

Force has a unit of Newton. A newton is defined as a kilogram-meter per second per second or $kg-m/sec^2$. This unit when multiplied by the unit of distance i.e. meter or m, we get $kg-m-m/sec^2$ or $kg-m^2/sec^2$. This can also be written as $kg (m/sec)^2$, but m/sec is the unit of velocity hence the unit of work is equal to the unit of mass times the square of the unit of velocity, or $w=mv^2$.

It is true that velocity is a vector quantity, therefore one might speak of -v and +v, but the unit of work involves the square of the velocity. The square of a positive number (+v) (+v) and the square of a negative number (-v)(-v) are both positive ($+v^2$), as we know from elementary algebra. Consequently, the square of the velocity involves no differences in signs and a unit that includes the square of the velocity is not a vector unit (unless it contains vector units other than velocity, of course).

We conclude then that work is a scalar quantity.

Work is a scalar quanity. This means it can be described by a simple number, which can be negative, zero or positive.

Is work scalar or vector ?

In the next section, we will look at the essence of work.